정팔각형의 꼭짓점을 반시계 방향으로 $A$, $B$, $C$, $D$, $E$, $F$, $G$, $H$라 하자. 또, 앞뒤가 나올 확률이 같은 동전이 하나 있다. 점 $P$가 최초에 점 $A$에 위치하고 있고, 다음의 시행을 10회 반복한다.
시행 : 동전을 던져 앞면이 나오면 점 $P$를 반시계방향으로 한 칸 움직이고, 뒷면이 나오면 시계방향으로 한 칸 움직인다.
이때, 다음의 두 사건을 생각하자.
사건 $S$ : 10번의 시행 후에 점 $P$가 점 $A$에 위치한다.
사건 $T$ : 10번의 시행을 하는 동안에 점 $P$가 적어도 한 번 점 $F$에 위치한다.
(1) 사건 $S$가 일어날 확률을 구하시오.
(2) 사건 $S$와 사건 $T$가 둘 다 일어날 확률을 구하시오.
생각해보기
(1)은 사건 $S$가 일어나는 경우를 나누어서 따져보면 어렵지 않게 해결할 수 있지만, (2)는 (1)에서 경우를 더 나누어서 생각해야 하므로 어렵다.
케이스를 나누는 방법이 여러가지가 있겠지만, 몇 가지 시도를 해보면 $P$가 점 $F$에 도달하는 때는 홀수번 째일 수 밖에 없다는 결론에 도달할 수 있을 것이다. 거기까지 생각이 미쳤다면, 이제 그 홀수에 따라 경우를 나누어 따지면 될 것 이다.
풀이
(1)
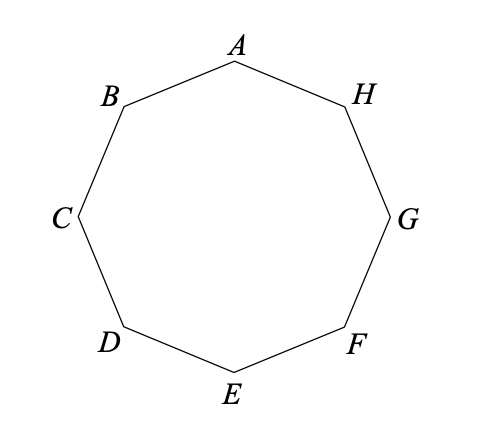
사건 $S$가 일어나는 경우는, 점 $P$가 반시계 방향으로 한 바퀴 도는 경우, 시계 방향으로 한 바퀴 도는 경우, 그리고 둘 다 아닌 경우의 3가지 경우로 나눌 수 있다. 각 경우에 대해 동전이 다음과 같이 나와야 한다.
(a) 앞면 9회, 뒷면 1회
(b) 앞면 1회, 뒷면 9회
(c) 앞면 5회, 뒷면 5회
이제 (a), (b)의 경우의 수는 각각 ${}_{10}C_9=10$이고, (c)의 경우의 수는 ${}_{10}C_5=252$이므로,
사건 $S$가 발생할 확률은, $$\cfrac{10+10+252}{2^{10}}=\cfrac{17}{64}$$이다.
(2)
(1)에서 (a), (b)의 경우는 점 $P$가 한 바퀴를 이동하므로 반드시 사건 $T$ 발생한다. 즉, 그 경우의 수는 20가지.
이제 (c)의 상황에서 점 $F$를 지나는 경우를 생각해보자.
도중에 점 $F$에 도달하는 경우는 홀수번 째이고, 1번째와 9번째에는 도달할 수 없다. (10번째에 $A$로 돌아갈 수 없음)
① 3번 째에 처음으로 점 $F$에 도달하는 경우
처음 3번 연속해서 뒷면이 나오고, 그 이후에 앞면 5번 뒷면 2번이 나오면 된다.
따라서 그 경우의 수는 ${}_{7}C_2=21$
② 5번 째에 처음으로 점 $F$에 도달하는 경우
처음 5번에서 [앞뒤뒤뒤뒤] , [뒤앞뒤뒤뒤], [뒤뒤앞뒤뒤] 중 하나가 나오고 그 이후에 앞면 4번 뒷면 1번이 나오면 된다.
따라서 그 경우의 수는 $3 \times {}_5C_1=15$
또, [앞앞앞앞앞뒤뒤뒤뒤뒤]의 1가지 경우가 더 있다.
③ 7번 째에 처음으로 점 $F$에 도달하는 경우
7번 째에 처음으로 점 $F$에 도달하고 10번 째에 점 $A$로 돌아 가기 위해서는, 어떤 경우든 마지막 절차가 $$H\rightarrow G\rightarrow F\rightarrow G\rightarrow H\rightarrow A$$ 일 수 밖에 없다. 따라서 처음 5번 중 앞면 2번 뒷면 3번이 나오고, 그 이후의 5번은 [뒤뒤앞앞앞]이 나와야 된다.
단, [뒤뒤뒤앞앞뒤뒤앞앞앞]은 ①의 경우에 포함되기 때문에, 총 경우의 수는 ${}_5C_2-1=9$
①,②,③에 의해 구하는 확률은 $$\cfrac{20+21+15+1+9}{2^{10}}=\cfrac{33}{512}$$
'본고사' 카테고리의 다른 글
| 도쿄대 2019-1(이과) (0) | 2021.12.02 |
|---|---|
| 도쿄대 2019-4(문과) (0) | 2021.11.24 |
| 도쿄대 2019-2(문과) (0) | 2021.09.29 |
| 도쿄대 2019-1(문과) (이과2) (0) | 2021.09.26 |
| 오사카대 2020-5(이과) (0) | 2021.09.22 |