교토대 2020-1(문과)

 

 

 

 

 곡선 $C:y=|x|x-3x+1$와 직선 $l:y=x+a$의 그래프가 접하게 되는 음의 실수 $a$의 값을 구하시오.
그리고 이 때, $C$와 $l$로 둘러싸인 부분의 넓이를 구하시오.

 

 

 

생각해보기

 

루트가 들어가는 마지막 적분 계산 실수 정도만 하지 않는다면, 무난히 풀 수 있는 문제일 것이다.

 

 

 

 

풀이

 

$x\ge 0$ 일 때, $y=x^2-3x+1={(x-\frac{3}{2})}^2-\frac{5}{4}$

 

$x<0$ 일 때, $y=-x^2-3x+1=-{(x+\frac{3}{2})}^2+\frac{13}{4}$

 

이므로 그래프를 그려보면 아래와 같다. $a$가 음수이기 때문에 $l$이 접하는 함수는 $x\ge 0$일 때의 함수이다.

$y=x^2-3x+1$에서 $y^{\prime }=2x-3=1$이므로 $x=2$에서 $C$와 $l$이 접한다. 접점의 좌표가 $(2,-1)$이므로 $a=-3$이다.

 

 

 

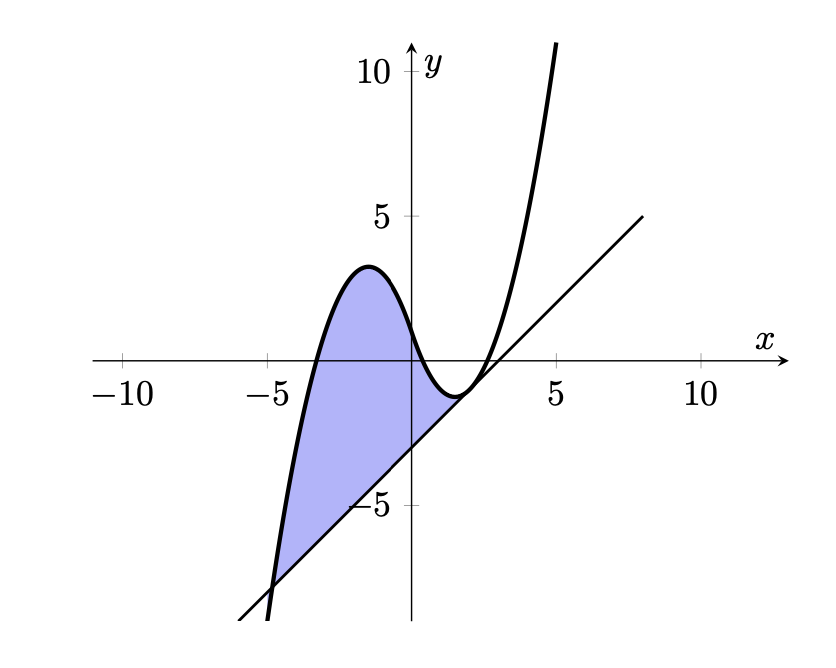
$C$의 $x<0$인 부분과 $l$의 접점을 먼저 구해보면,

$$-x^2-3x+1=x-3x^2+4x-4=0x=-2\pm 2\sqrt{2}$$

$x<0$에서 $x=-2-2\sqrt{2}$ 이다.

 

$C$와 $l$ 사이의 넓이를 정적분으로 구하면, 

$$\begin{array}{rl}& {\int }_{-2-2\sqrt{2}}^0\{(-x^2-3x+1)-(x-3)\}dx+{\int }_0^2\{(x^2-3x+1)-(x-3)\}dx\\ =& {\int }_{-2-2\sqrt{2}}^0(-x^2-4x+4)dx+{\int }_0^2(x^2-4x+4)dx\\ =& {\int }_{-2-2\sqrt{2}}^0\{-(x+2{)}^2+8\}dx+{\int }_0^2(x-2{)}^{2}dx\\ =& {\left[\frac{(x-2{)}^3}{3}\right]}_0^2+{[-\frac{(x+2{)}^3}{3}+8x]}_{-2-2\sqrt{2}}^0\\ =& 16+\frac{32}{3}\sqrt{2}\end{array}$$