오사카대 2020-4(이과)

 

 

 

 

 

양의 실수 $t$에 대해, 아래 연립부등식이 나타내는 영역의 넓이를 $S(t)$라고 하자.
$$x\ge 0,y\ge 0,xy\le 1,x+y\le t$$
이때, ${\displaystyle \underset{t\to \mathrm{\infty }}{lim}(S(t)-2\log t)}$를 구하시오.

 

 

 

 

 

 

생각해보기

 

 

우리나라 학생들에게 여전히 낯선 부등식의 영역 문제이다. $t$의 값에 따라 생기는 영역의 모습이 변할까봐 고민하지말자. 어짜피 구하는 극한값은 한없이 큰 $t$에  극한값이므로, 적당히 크고 일반적인 $t$에 대한 그래프의 개형에서 출발하면 충분하다.

 

 

 

 

 

 

풀이

 

 

$t>2$에 대해, 주어진 부등식의 영역을 나타낸 그래프는 아래와 같다.

 

 

 

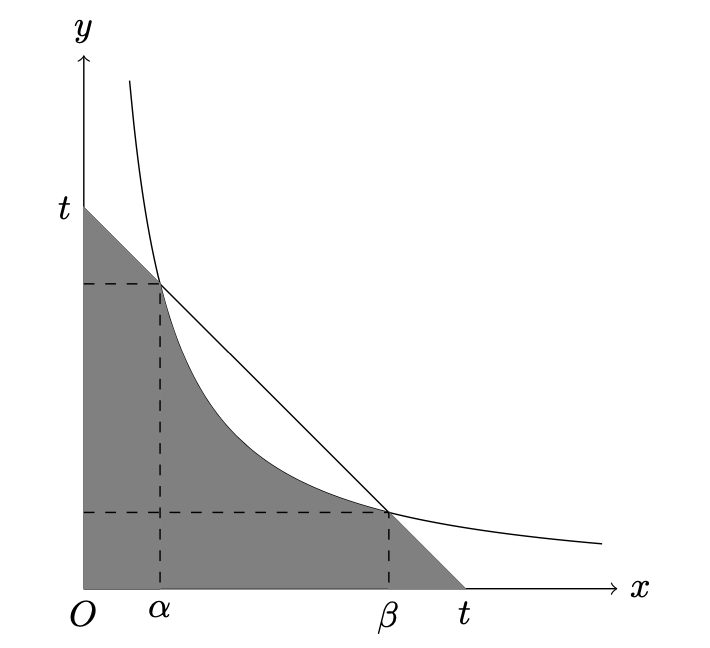
먼저 영역의 경계인 두 식 $xy=1$과 $x+y=t$를 연립하면, 

$$x(t-x)=1,x^2-tx+1=0$$

에서 두 근을 $\alpha ,\beta (\alpha <\beta )$라 하면, 

$$\alpha =\frac{t-\sqrt{t^2-4}}{2},\beta =\frac{t+\sqrt{t^2-4}}{2}$$

이다. 이때, 영역의 넓이 $S(t)$는

$$\begin{array}{rl}S(t)& =\frac{1}{2}{t}^2-{\int }_{\alpha }^{\beta }(t-x-\frac{1}{x})dx\\ & =\frac{1}{2}{t}^2-t(\beta -\alpha )+\frac{1}{2}({\beta }^2-{\alpha }^2)+\log \beta +\log \alpha \\ & =\frac{1}{2}{t}^2-t\sqrt{t^2-4}+\frac{1}{2}t\sqrt{t^2-4}+\log \frac{t+\sqrt{t^2-4}}{t-\sqrt{t^2-4}}\\ & =\frac{1}{2}{t}^2-\frac{1}{2}t\sqrt{t^2-4}+\log \frac{(t+\sqrt{t^2-4}{)}^2}{4}\\ & =\frac{1}{2}t(t-\sqrt{t^2-4})+2\log \frac{t+\sqrt{t^2-4}}{2}\end{array}$$

이다. 이제, $S(t)-2\log t=\frac{1}{2}t(t-\sqrt{t^2-4})+2\log \frac{t+\sqrt{t^2-4}}{2t}$이므로,

 

$$\begin{array}{rl}\underset{t\to \mathrm{\infty }}{lim}(S(t)-2\log t)& =\underset{t\to \mathrm{\infty }}{lim}(\frac{1}{2}t\cdot \frac{4}{t+\sqrt{t^2-4}}+2\log \frac{t+\sqrt{t^2-4}}{2t})\\ & =\underset{t\to \mathrm{\infty }}{lim}(\frac{2}{1+\sqrt{1-\frac{4}{t^2}}}+2\log \frac{1+\sqrt{1-\frac{4}{t^2}}}{2})\\ & =1\end{array}$$