복소수 $\alpha$, $\beta$, $\gamma$, $\delta$와 실수 $a, b$가 다음의 세 조건을 만족하면서 움직인다.
조건 1 : $\alpha$, $\beta$, $\gamma$, $\delta$는 서로 다르다.
조건 2 : $\alpha$, $\beta$, $\gamma$, $\delta$는 4차 방정식 $z^4-2z^3-2az+b=0$의 근이다.
조건 3 : $\alpha \beta + \gamma \delta$의 실수부는 0이고, 허수부는 0이 아니다.
(1) $\alpha$, $\beta$, $\gamma$, $\delta$ 중 2개는 실수이고, 나머지 2개는 서로 켤레복소수임을 보이시오.
(2) $b$를 $a$로 나타내시오.
(3) $\alpha +\beta$가 취할 수 있는 값의 범위를 복소평면 위에 나타내시오.
생각해보기
(1)은, 4개의 복소수가 실수 계수의 4차 방정식의 근이므로, 허근이 있다고 한다면 2개나 4개입니다. 켤레복소수도 같은 방정식의 해가 된다는 사실을 이용하면 보일 수 있습니다.
(2)는, 방정식의 계수를 이용하여 구할 수 있습니다. 문자와 식이 많이 나와서 혼란스럽기 떄문에, 먼저 (1)의 결과를 이용하여 4개의 복소수를 4개의 실수로 나타내는 것이 좋습니다.
(3)은 자취의 방정식문제인데, (2)에서 유도한 식을 이용할 수 밖에 없습니다.
풀이
(1)
조건 3에 의해 $\alpha$, $\beta$, $\gamma$, $\delta$ 중 적어도 하나는 허수이다. $\alpha$를 허수라고 할 때, 조건 2에서 $\alpha$는 실수 계수인 4차 방정식의 한 근이므로 켤레복소수 $\bar{\alpha}$도 이 방정식의 근이 된다. 따라서 $\beta$, $\gamma$, $\delta$ 중 하나가 곧 $\bar{\alpha}$이다.
먼저 $\beta = \bar{\alpha}$이면, $\gamma$, $\delta$는 모두 실수이거나 서로 켤레복소수이다. 이때 $\alpha \beta + \gamma \delta$는 실수가 되어 조건 3을 만족할 수 없다.
따라서 $\gamma$, $\delta$ 중 하나가 $\bar{\alpha}$이고, $\gamma = \bar{\alpha}$라 해도 일반성을 잃지 않는다.
여기서 만약 남은 두 수가 허수라면, $\delta = \bar{\beta}$이고
$$\begin{align} &\overline{\alpha \beta + \gamma \delta}\\=&\overline{\alpha \beta + \overline{\alpha \beta}}\\=&\overline{\alpha \beta}+\alpha \beta\\=&\alpha \beta + \gamma \delta \end{align}$$
이므로 $\alpha \beta +\gamma \delta$가 실수가 되어 조건 3을 만족하지 않는다. 따라서 $\beta$, $\delta$는 실수이다.
이상으로 $\alpha$, $\beta$, $\gamma$, $\delta$ 중 2개는 실수이고, 나머지 2개는 켤레복소수임을 알 수 있다.
(2)
(1)에서 논의한 내용을 통해서 우리는 $\alpha$, $\beta$, $\gamma$, $\delta$를 네 실수 $p,q,r,s$를 사용해 나타낼 수 있다. 다시 말해서 $\alpha$와 $\beta$는 $p+qi$, $r$로 그리고 $\gamma$와 $\delta$는 $p-qi$, $s$로 써도 무방하다. 단, 조건 1로 부터 $q \neq 0$이고 $r \neq s$를 만족해야 한다.
$$\begin{align} &\alpha \beta +\gamma \delta \\=&r(p+qi)+s(p-qi)\\=&p(r+s)+q(r-s)i\end{align}$$
이므로 조건 3에서, $p(r+s)=0$이다.
조건 2에서 $\alpha$, $\beta$, $\gamma$, $\delta$는 $z^4-2z^3-2az+b=0$의 근이므로, 인수정리에 의해 방정식의 좌변을
$$\begin{align} &(z-p-qi)(z-p+qi)(z-r)(z-s)\\=&\left\{ z^2 -2pz+(p^2+q^2)\right\}\left\{z^2-(r+s)z+rs\right\}\end{align}$$로 나타낼 수 있다.
먼저 $z^2$의 계수를 비교하면 $$(p^2 +q^2 )+rs+2p(r+s)=0$$인데, 조금 전에 $p(r+s)=0$임을 보였기 때문에, $$ p^2 +q^2 =-rs \qquad \cdots (\star)$$라는 사실을 얻을 수 있다.
이어서 $z^3$의 계수를 비교하면 $$-2p-(r+s)=-2$$를 얻는다. 마찬가지로 조건3에서 $p(r+s)=0$였기 때문에, $p=0$이면 $r+s=2$이고, $r+s=0$이면 $p=1$임을 알 수 있다.
상수항을 비교하면 $$\begin{align} rs(p^2 +q^2 )&=b\\-r^2s^2&=b \end{align}$$
이고, 마지막으로 $z$의 계수를 비교하면 $$\begin{align} -2prs-(p^2 +q^2)(r+s)&=-2a\\-2prs+rs(r+s)&=-2a\\rs\left\{-2p+(r+s)\right\}&=-2a\end{align}$$이다. 위 식으로부터 $p=0$, $r+s=2$일 때는 $a=-rs$이고, $p=1$, $r+s=0$일 때는 $a=rs$임을 알 수 있다. 어느 경우든 $r^2s^2=a^2$이므로 $$b=-r^2s^2=-a^2$$가 된다.
(3)
(2)에서 논의한 내용을 계속 이어나가자.
① $p=1$, $r+s=0$일 때
$(\star)$로 부터,$$ 1+q^2 =-r(-r)=r^2$$가 성립한다. 이를 만족하는 $r$, $q$ 중에서 $q \neq 0$인 쌍을 정하면, 복소수 $\alpha$, $\beta$, $\gamma$, $\delta$와 실수 $a$, $b$가 정해지고 3개의 조건도 만족함을 알 수 있다.
$\alpha +\beta=X+Yi$라 하면, $$1+r=X,\quad q=Y$$이므로 자취의 방정식은 $$ (X-1)^2 -Y^2=1$$이다.
② $p=0$, $r+s=2$일 때
$(\star)$로 부터, $$q^2=-r(2-r)=(r-1)^2-1$$가 성립한다. 이를 만족하는 $r$, $q$ 중에서 $q \neq 0$인 쌍을 정하면, 복소수 $\alpha$, $\beta$, $\gamma$, $\delta$와 실수 $a$, $b$가 정해지고 3개의 조건도 만족함을 알 수 있다.
$\alpha +\beta =X+Yi$라 하면, $$r=X,\quad q=Y$$이므로 자취의 방정식은 $$(X-1)^2 -Y^2 =1$$이다.
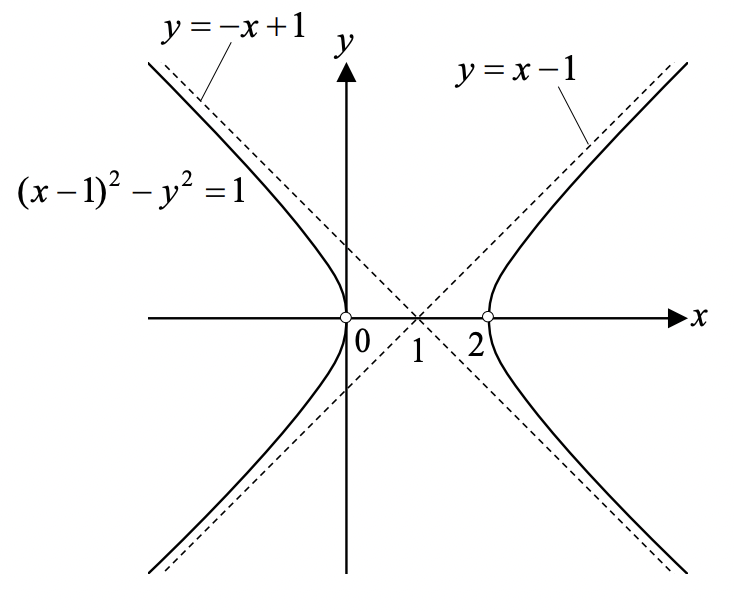
이상에서 복소수 $\alpha +\beta$가 성립하는 범위는, 쌍곡선 $(X-1)^2 -Y^2 =q$에서 $Y=0$인 점은 제외한 부분이다.
'본고사' 카테고리의 다른 글
| 교토대 2019-2(문과) (0) | 2022.05.16 |
|---|---|
| 교토대 2019-1(문과) (1) | 2022.03.16 |
| 도쿄대 2019-5(이과) (0) | 2022.01.25 |
| 도쿄대 2019-4(이과) (0) | 2022.01.22 |
| 도쿄대 2019-3(이과) (0) | 2021.12.14 |